Variable Types
Information is stored within variable objects. A variable object is akin to a shelving concept described by
- a name - which starts with lower or upper case letter. R program is unable to create variable names starting with numbers or special characters e.g.
_. The name may involve numbers or_following the first letter e.g.x1orx_1. - an encasement to hold data, and
- contents inside the encasement.
Naming System
It is essential to set up variable names according to a methodical or systematic naming practice. For instance, variables associated with a particular data type e.g. balance sheet or health insurance, etc. to start with a common letter and more desirably compact representations such as hins_partA_01, hins_partB_01, etc. This enables more efficient workspace management as well as better collaborative workflow optimization.
The three aspects above fully characterise a variable object that is ready to be called or used for computations.
Assignment Operators = & <-
Variables are populated based on software user inputted values or imported data. The former is carried out according to two approaches:
-
Using '=' such as
x = 1instructs the software store the right-hand-side value into the left-hand-side space. Within the context of R language, '=' is considered a weaker assignment instruction or under certain condition a temporary assignment. Consider the example below where variablexis defined within an outer commandmean(). in this case, the variable is defined and used for computing the average and referred to as a subexpressions but discarded immediately after without appearing in the software workspace for future use. -
Assign a value to a name
<-(leftwards): This operator is applicable anywhere and encompasses the functionality of=in addition to ensuring the values are stored under the workspace.
| Calling x in line 2 returns error | |
|---|---|
1 2 | |
| Calling x in line 2 returns values | |
|---|---|
1 2 | |
In general both assignments are considered acceptable, however, note that the developer may intentionally aim for temporary use of variables and under such circumstances, using = is considered optimal since it leads to lower memory usage.
Re-using, Over-writing and Re-allocating
R language permits redefining a variable contents, without prompting a notice. This is considered a convenient feature when attempting to correct the content of a preexisting variable without encountering an error or requiring additional lines of code to confirm overwriting operation.
However, a developer should exercise causion when naming variables since unintended overwrites can also take place without notifying the developer.
Missing Values and Special Entries
- NaN: 'Not a Number' arises across numeric variables when a non-numeric e.g. text, date, etc. appears along the entries.
- NULL: Represents an object with zero length. This reflects a case where no allocation has been made contrary to the NaN where allocation is made with empty data stored
- NA:
The following commands enable verifying the variables versus each of the three outcomes above. Note that the result of this verification is reported under the console panel and in a form of a True or False (logical) output:
Encasement and Contents
 For instance, the first row from the bottom and the second column in the illustration below is a location address to the bookshelf. Given that the shelving is in place, an array exists to hold contents. The contents in the location is the data, e.g. the numeric value 3.14 in the shelving. When the contents under the shelving is missing, then that value appears as NaN, whereas when the entire bookshelf is missing, the variable name is associated with a NULL. The contents under row one across column 3 is a text entry 'Pi' which is interpreted as NaN by the software.
For instance, the first row from the bottom and the second column in the illustration below is a location address to the bookshelf. Given that the shelving is in place, an array exists to hold contents. The contents in the location is the data, e.g. the numeric value 3.14 in the shelving. When the contents under the shelving is missing, then that value appears as NaN, whereas when the entire bookshelf is missing, the variable name is associated with a NULL. The contents under row one across column 3 is a text entry 'Pi' which is interpreted as NaN by the software.
When interacting with numerical variables such as discrete or continuous type data, it is possible to encounter two special cases amongst the variable entries:
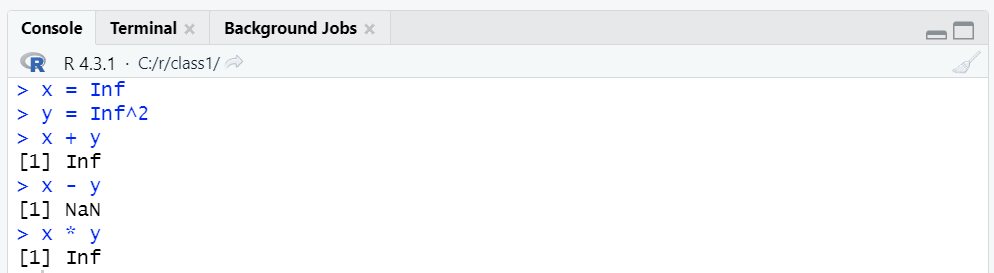
- Inf: The computer scientific definition of the infinity value in R program is 1e308 i.e. \(10^{308}\). Any value larger than the threshold value is stored as
Infwhere calculus operations associated withInflead to a trivial outputs mapping either toInf(disregarding power of magnitude) or alternative NaN as a counterbalancing result. As a side note, further operations will be possible via Analytical Algebraic System where values are inputted as symbolic entries (explained later) further enabling extended computations such as computing values at limits based on the order of magnitude.
- Complex: While there exists several context to apply the complex numbers (e.g. working with characteristics function in statistical analysis), the applications within the current course are rare. However, a complex entry may be encountered within regular applications due to errors in computations such as when an optimization outcome for variance estimation returns a negative value due to that numerical value achieving a maximum objective while in fact there is no real-value interpretations. Such cases may later result in encountering a complex entry since the square root of the incorrectly estimated variance over the negative real line corresponds to a complex values standard error.
| Encountering Complex Values | |
|---|---|
1 2 | |
Complex numbers are rarely used in the context of this course, however it is important to be familiar with their overall appearances as a method of troubleshooting coding routines as they may still arise due to computational reasons.